研究者対象 葉面積指数(LAI)完全ガイド #2
「LP-80によるLAIの求め方、より詳しく知りたい方へ」

Dr. Gaylon S. Campbell
葉面積指数(LAI)は、ある特定の時間に撮影されたキャノピーの統計的スナップショットという、たった一つの数値に過ぎません。しかし、この1つの数値が、放射の遮断、エネルギー変換、運動量、ガス交換、降水の遮断、蒸発散など、キャノピーの主要なプロセスをモデル化し理解するために使用されるため、重要な洞察につながる可能性があります。
旧来のLAI法は面倒
葉面積指数は、単位地上面積当たりの樹冠または植物群落の片面緑葉面積として定義されます。これは、キャノピーの単位面積の地面を覆うすべての葉を収穫し、その面積を測定することによって求めることができます。1981年、Andersonは、より破壊的でないLAIを求める方法を開発しました。上方を向いた半球状の写真を使い、キャノピーを透過する光の割合を推定し、予測的な数学モデルを適用して葉面積指数を推定しました。
魚眼レンズで撮影したキャノピー写真を評価するのは、とても面倒な作業でした。通常、アシスタントが各写真の上にグリッドを置き、四角のうち何パーセントが光であるかを数えます。ある研究員は、「何時間も写真を見ていると、チェッカーの夢を見たものです」と振り返ります。この「チェッカー」によって、ランダムな光線がキャノピーの特定の部分を透過する確率を求めることができたのです。
LAIの換算
葉面積指数の値を得ることは、多くの場合、その途中のポイントに過ぎません。キャノピーの環境相互作用をモデル化するためにLAIを使用する場合、光合成有効放射量(PAR)を測定する方がより直接的な方法かもしれません。というのも、これらのモデルの多くは、そもそもPARを予測するためにLAIを使用しているからです。PARを用いてLAIを推定することは可能です。しかし、PARが本当に欲しい数値であるなら、なぜそうするのでしょうか?LAIがあなたの特定のアプリケーションに最も有用なパラメータであるかどうかを評価したくなるのではないでしょうか。単純に取得されたPARを測定し、そのデータを直接適切なモデルで使用する方が、より簡単で、通常より正確な場合があるからです。
この光の割合を葉面積指数に変換する数学的モデルは、比較的単純です。その仕組みを理解するために、10平方センチメートルの面積の葉を大きな白い正方形の上に水平に置くことを思い浮かべてください。そうすると、10平方センチメートルの影ができます。次に、同じ大きさの葉をランダムに正方形にかぶせます。このとき、葉が重なる可能性はありますが、確率的には20平方センチメートルの影ができるはずです。3枚目の葉を入れると、重なる確率が高くなります。さらに葉をランダムに配置していくと、最終的には白い正方形が完全に影になります。また、葉を増やすと葉の面積は増えますが、すべての光を遮ったため、日陰の面積は一定に保たれます。
LP-80 がその方程式を解く
この現象を説明する方程式(数学的な導出は下の「方程式の解法」を参照)は次の通りです。
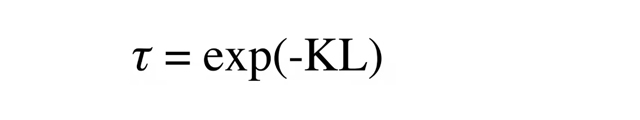
τは光線がキャノピーを透過する確率、L はキャノピーの葉面積指数、K はキャノピーの減衰係数です。晴れた日にキャノピーの上と下の光合成有効放射量を測定すると、両者の比(下の光合成有効放射量と上の光合成有効放射量)は、ほぼτに等しくなります。
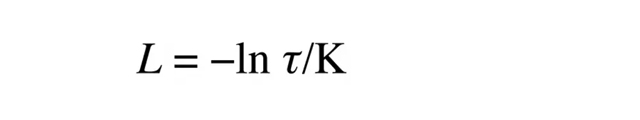
LP-80は基本的にこの方程式を解いて葉面積指数を求めます。しかし、いくつか複雑な要因があります。モデルを構築する際、人工キャノピーの葉は水平で黒く、すべての放射が太陽から直接届くと仮定しました。実際には、太陽の角度は一日のうちで変化しますし、実際のキャノピーはかなり複雑な構造になっています。また、キャノピーの葉や空から散乱される放射もあります。光合成有効放射量の測定値から葉面積指数を求める完全なモデルには、これらすべての要因の補正が含まれています。
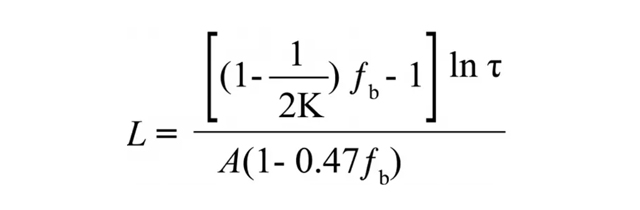
この式はLP-80で実際に使われているもので、葉に吸収される(散乱されない)光の量をA の項で、キャノピーにビームとして入射する光の割合をƒb の項で調整しています。キャノピーの減衰係数であるK は、太陽の天頂角と葉の分布に関する変数を含んでいます。位置を指定し、内部時計をローカルタイムに設定すると、LP-80は各測定時の太陽の天頂角を計算します。葉の角度分布は、特に指定がない限り、球形と仮定します。
方程式の解法
ランダムに分布する黒い葉の樹冠を、各層の葉面積が限りなく小さくなるように多くの層に分けると(dL )、その層の最上部から最下部までの放射の変化は以下の式になります。
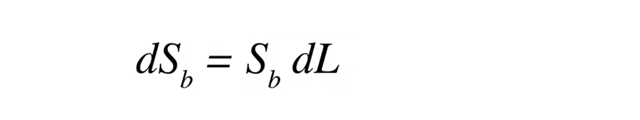
つまり、キャノピーのこの部分を通過する太陽光の平均量の変化(dSb )は、単位面積当たりの平均放射電力量(Sb )に葉面積指数の変化(dL )をかけた負の値に等しい(葉面積が大きくなると光量が減少するため)です。これは変数分離可能な微分方程式です。両辺をSb で割って、キャノピー上端から下に向かって積分すると、次のようになります。
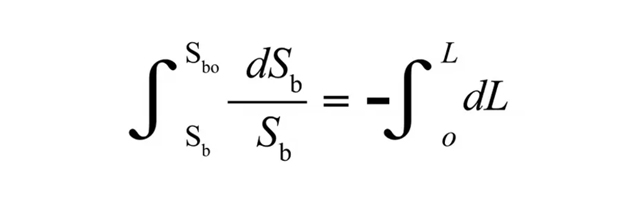
積分を実行すると、
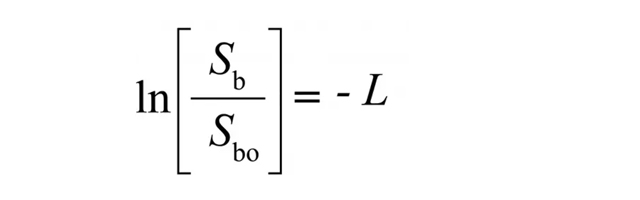
両辺のべき乗をとると、
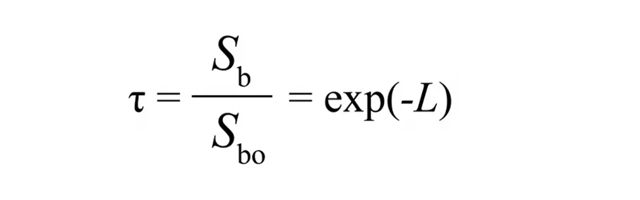
Sbo はキャノピー上部の水平面上の放射、τは光線がキャノピーを透過する確率、キャノピー下部のビーム放射と上部のビーム放射の比と同じです(キャノピー内で放射の散乱がないと仮定しているため)。水平でない葉を持つキャノピーの場合、L をKL に置き換える以外は結果は同じで、K はキャノピーの減衰係数です。
参考文献
Anderson, Margaret C. “The geometry of leaf distribution in some south-eastern Australian forests.” Agricultural Meteorology 25 (1981): 195-206. Article link.
LP-80:その精度は?
LP-80は、キャノピーの光合成活動放射量(PAR)を高速で直接測定します。電源を入れるとすぐにPARが測定され、葉面積指数(LAI)の測定も可能です。しかし、このLAIの測定はどこから来るのでしょうか、またその精度はどうなのでしょうか?
キャノピーは変化しやすい。LP-80はそれをχ で説明します。
葉面積指数とは、キャノピーや植物群落の単位地上面積あたりの片面緑葉面積のことです。LAIを直接測定するには、キャノピーの単位地上面積より上の部分の各葉の面積を測定する必要があります。この方法は破壊的であり、また非常に時間がかかるため、ほとんど使用されていません。半球体写真から光学センサーまで、葉面積指数の他のすべての測定は、この値を近似化することを試みています。LP-80は、光合成有効放射量を測定し、そのPAR値を葉面積指数に変換することによりLAIを求めます。LP-80は、葉面積指数を計算するためにいくつかの変数を使用します。その中の一つ、χ はキャノピー内の葉の向きを表す変数です。
χ とは?
χ は、"キャノピー角度分布パラメータ "です。これは、キャノピーの構造、つまり葉が空間内でどのような方向を向いているかを表しています。つまり、キャノピーの各葉の向きを変えずに注意深く動かすと、その葉で球体の表面を覆うことができるのです。葉が球状に分布しているキャノピーは、χ 値が1になります。
多くのキャノピー構造は、より水平( χ > 1)または垂直( χ < 1)になる傾向があります。キャノピーの種類によっては、χ 値が公表されているものもあります(簡単なリストはLP-80のマニュアルをご覧ください)。しかし、この値は種によって異なる可能性があるため、値を近似化できることが重要です。
LAIとPAR: どちらが先か?
葉面積指数の値を得ることは、多くの場合、その途中のポイントに過ぎません。キャノピーの環境相互作用をモデル化するためにLAIを使うのであれば、光合成有効放射量(PAR)を測定する方が近道かもしれません。なぜなら、これらの数学的モデルの多くは、その内部方程式でPARを予測するためにLAIを使用しているからです。研究者がLAIを予測するためにPARを使用し、その後、知らず知らずのうちにLAIの数値をモデルに入れ、逆にLAIを予測することがあるのです。特定の用途において、LAIが最も有用なパラメータであるかどうかを評価することは重要です。単に捕獲されたPARを測定し、そのデータを適切なモデルで直接使用する方が、より簡単で、通常より正確な場合があります。
良いχ 値はLAI近似の精度を向上させる
χ は、少なくとも小数点以下2桁の正確な数値が欲しいところです。しかし、キャノピーには驚くほどのばらつきがあるため、このような精度を達成することは不可能です。葉面積指数の数値は貴重ではあるものの、常に近似値に過ぎません。良いχ 値は、この葉面積指数(LAI)近似値の精度を向上させます。しかし、精度の低いχ 値でも、他の条件次第では、葉面積指数近似値はおそらくかなり正確になるでしょう(図1参照)。
キャノピーのχ 値を近似するには、深さと幅が同じであるキャノピーの代表的な塊を見つけます。次に、垂直方向の隙間率(τ0 )-塊を通して垂直方向に見える光と影の割合-と水平方向の隙間率(τ90 )-塊を通して水平方向に見える光の割合-を求めます。例えば、葉が完全に垂直なキャノピーでは、水平方向に約10%の光と90%の影を見ることができ、(τ90 )=0.1、垂直方向に100%の光を見ることができると(τ0 )=1と考えられます。χ は次の簡単な式から求められます。
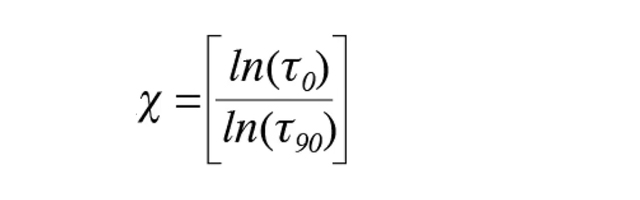
この式を用いると、完全に垂直なキャノピーであればχ = 0となります。もし、葉が球状に分布し、垂直方向にも水平方向にも約10%の光が見えるとしたら、(τ90 ) = (τ0 ) = 0.1 となります。そこで、この式を使ってχ = 1とします(ちなみに、LP-80のχ の初期設定はこれです)。
最終的なLAI値の不確かさを最小にする
キャノピーの「代表的な塊」を通して見える光の量を推定することは、現実的には難しいかもしれません。背景を作り、それを使ってキャノピーを分析する方が簡単かもしれません(私たちは1メートル×1メートルの正方形の色付きポスターボードを使いました)。その塊は、キャノピーの典型的な要素をすべて含んでいなければなりません。例えば、列作物を研究している場合、塊はある列の中心から次の列の中心までで、列と列の間に生じる、キャノピーの特徴的な隙間を含むようにする必要があります。塊を立方体に分解することを想像してください。τを見積もるには、背景を使って立方体の裏側を作り、表側に立って、キャノピーの立方体部分を水平方向に透過する光の割合を見積もります。τ0を推定するには、背景を立方体の上部または下部のいずれかに配置し、反対側の端に自分自身を置いて、垂直方向に透過する光の割合を推定します。そして、式1(上図)からχ を求めます。
水平方向のキャノピーのχ 値は1より大きく、垂直方向のキャノピーのχ 値は1より小さいことを覚えておき、推定値の妥当性を確認します。キャノピーのχ 値は、LP-80のセットアップメニューの「χ 設定」を選択することで指定できます。この方法を用いれば、最終的な葉面積指数値の不確かさを最小にするχ 値を推定することができるはずです。
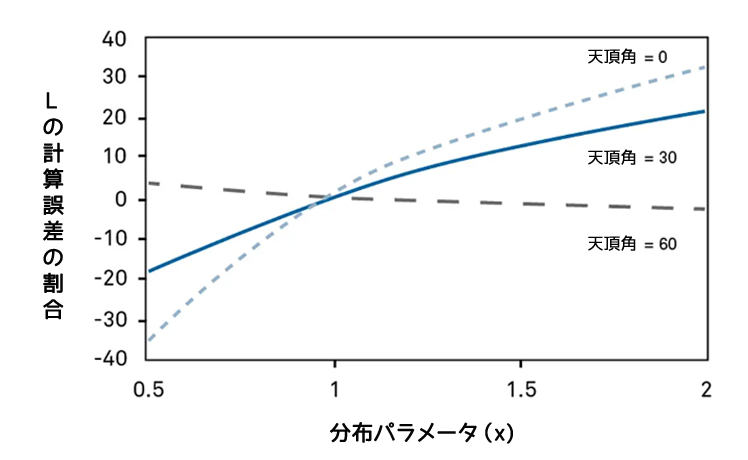
この図は、LP-80でχ = 1とし、実際のキャノピーの分布パラメータが図のような値だった場合のLの計算誤差のパーセントを示したものです。完全な日射(ƒb = 0.8)を想定しています。誤差は太陽の天頂角に依存することに注意してください。ほとんどの測定は天頂角30度以上で行われますので、キャノピーの分布パラメータ情報を持たない完全太陽での誤差は、最悪でも20%です。この誤差はƒb の値が小さくなるにつれて減少し、ƒb がゼロのときにゼロとなります。もし、キャノピー分布パラメータが10%以上の精度で推定できれば、天頂角がゼロの場合でもLAIの誤差は5%以下になります。したがって、分布パラメータの不確かさは、LAIの不確かさに大きく寄与しないと考えられます。
植物による炭素同化の簡略化されたモデル
Dr. Gaylon S. Campbell
光合成の詳細なプロセスは複雑で、モデル化するのが難しいです。しかし、多くの場合、同化の制限のうち1つ以上に着目することで、モデルを単純化することが可能です。
炭素同化の簡略化:光と水
炭素同化とは、植物の葉の中で、二酸化炭素と水を炭水化物と酸素に化学変化させることです。このプロセスにはエネルギーが必要で、そのエネルギーは光(通常は太陽からの光)によって供給されます。大気中の二酸化炭素は、葉の葉緑体細胞内に拡散し、固定されます。葉の中は大気よりずっと湿っているので、CO2が拡散してくるのと同時に水も拡散していきます。実際の光合成で使われる水の量は微々たるものですが、CO2の取り込みに伴って失われる水の量は多いです。
光による制限と水による制限:2つのアプローチ
このような簡単な説明から、光が同化の制限因子となる場合と、水が制限因子となる場合が想定されます。つまり、同化は植物の光捕捉能力に比例し、同化は植物の水捕捉能力に比例する、というモデルです。どちらのアプローチも、バイオマス生産のモデリングに有用です。
光ベースモデル
光に基づくモデルを方程式で表すと次のようになります。
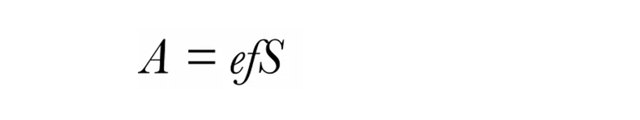
ここで、A は純乾物同化量、S は作物が生育している間に受けた全入射放射、ƒ は作物によって遮られた放射の平均割合、e は変換効率です。A とS がともにmol m-2s-1で表されている場合、e は無次元変換効率です。光制限のある状況では、e の値は特定の種についてかなり控えめで、0.01~0.03 mol CO2(mol photons)-1の範囲です。Campbell and Norman (1998, p. 237) は、より完全な分析を行うための追加情報と参考文献を提供しています。
ACCUPAR LP-80によるƒ の測定
植物キャノピーによって遮断された入射光の割合であるƒ は、同化を決定する上で重要な要素であることは明らかです。ACCUPAR LP-80は、このƒ を直接測定することができます。光に制限のある環境では、入射光量と光変換効率eを知り、LP-80で経時的にfを測定することで、乾物生産量を予測することができます。
水ベースモデル
水が制限された環境では、別の式が適用されます。それは以下の式になります。
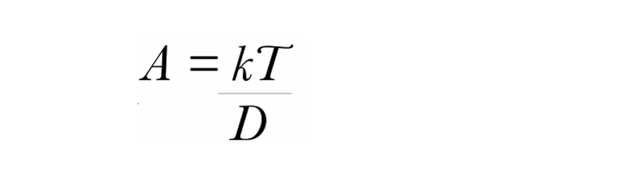
ここで、T は蒸散量、D は大気中の水蒸気不足量、k は特定の種と大気中のCO2レベルに対する定数です。この式の導出はTanner and Sinclair (1983) とCampbell and Norman (1998) が行っていますが、その妥当性は1世紀以上前の実験でも繰り返し確認されています。特に、湿度の高い地域では、乾燥地域よりも単位水量当たりの乾物生産量が多くなることが予測されます。したがって、たとえばウィスコンシン州で灌漑事業を行った場合、アリゾナ州で行った場合よりも単位水量あたりの乾物生産量が多くなるのです。生物種によって単位水量あたりの乾物生産量に差はありますが、乾物生産には大量の水が必要なのです。遺伝子操作して水を使わずに炭素を固定する植物を育てて砂漠に花を咲かせるというのは、単なる夢でしかありません。
水ベースモデルにおける遮蔽
蒸発に基づく乾物モデルは、光の遮断にも依存します。作物が失う水には、植物が蒸散する水と土壌から蒸発する水があります。炭素同化に関係するのは、蒸散によって失われる水だけです。通常、式2のT を測定することは現実的ではありませんが、雨や灌漑、いくつかの土壌や環境の変数がわかれば、毎日計算する簡単なコンピュータモデルを作成することができます。このモデルでは、ポテンシャル蒸発散量と呼ばれる量を定義する必要があります。これは、水の供給が蒸発も蒸散も制限しない場合の水の損失率です。ポテンシャル蒸散量は次の式で計算されます。
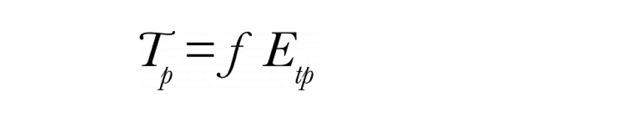
土壌表面からの蒸発も水を使うので、これも計算する必要があります。ポテンシャル蒸発量は次の式で計算されます。
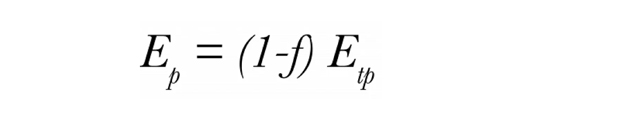
ここで、Etp はポテンシャル蒸発散量です。前述と同様に、ƒ はキャノピーで遮られた放射線の割合であり、LP-80で測定することが可能です。Campbell and Diaz (1988)は、Etp を計算するための簡単なコンピュータモデルと、式3および4で与えられる潜在量から実際の蒸発と蒸散を計算するためのアルゴリズムを提供しています。
どのモデルを使用するかを知るのは簡単です。
光と水のどちらが制限要因かを判断する最も効率的な方法は、単純に両方の数学的モデルを毎日実行し、どちらの予測値が最も低いかを確認することです。その値が、実行された特定の日の乾物生産量を最もよく予測する値です。
BASICコンピュータモデリング
光制限および水制限の数学モデルは、手作業で操作するのは難しいですが、コンピュータでプログラムするのは簡単です。簡単に入手できる気候データから実行でき、特に一年生作物では作物の乾物生産量をかなり正確に予測することができます。特に、特定の環境と文化的実践に対する生産能力を評価するのに有用です(Campbell and Diaz, 1988; Kunkel and Campbell, 1987)。
遮断率の計算
これらのモデルで使用される遮断率ƒ は、全日を平均した値です。LP-80による測定は、通常、特定の時間帯に行われるため、一日の平均値とはなりません。LP-80 のマニュアルには、単発の観測値から一日平均に変換するための式と例(P.57)が記載されています。LP-80は、キャノピー下で測定されたPARと上方で測定されたPARの比率を取ることによって放射の透過を測定します。これは、特定の太陽天頂角における透過率τ(θ) です。日間平均の透過率は、拡散放射の透過率と同じで、次式で与えられます。
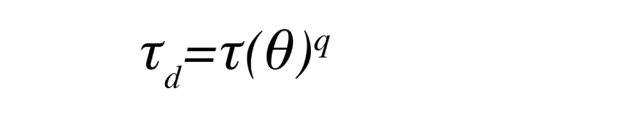
ここで、q はマニュアルにあるように、葉面積指数、葉の角度分布、太陽の天頂角に依存します。これらのモデルの遮蔽率は以下になります。
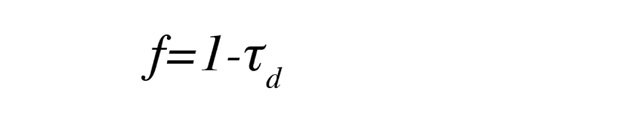
参考文献
Campbell, G. S., and R. Diaz. “Simplified soil-water balance models to predict crop transpiration.” Drought research priorities for the dryland tropics. ICRISAT, India (1988): 15-26. Article link (open access).
Campbell, G. S., and J. M. Norman. An Introduction to Environmental Biophysics (2nd Ed.). New York: Springer,1998. Article link.
Kunkel, Robert, and Gaylon S. Campbell. “Maximum potential potato yield in the Columbia Basin, USA: Model and measured values.” American potato journal 64, no. 7 (1987): 355-366. Article link.
LP-80のビーム率計算によるLAI測定の簡略化について
ACCUPAR LP-80のプローブに到達する放射は、太陽ビームから直接来る場合と、空や雲から散乱される場合があります。この2つの放射源はキャノピー構造によって異なる影響を受けるため、キャノピー透過率測定から葉面積指数(LAI)を計算する際には、別々に取り扱う必要があります。計算に必要な情報は、プローブに入射する全放射(ビーム+散乱または拡散PAR)に対するビーム率(太陽ビームから直接入射する放射の比率)です。
プローブの遮光が不要
従来のACCUPARでは、プローブを遮光してビーム・フラクションを測定する必要がありました。LP-80では、利用可能な測定値を使用して計算します。Spittersら(1986)が全放射線に対するビーム率を求めるために発表した方法を改良して使用しています。彼らは、全天候型放射線の測定値と地球大気圏外の水平面上の潜在放射線の比をビーム率として関連づけました。
LP-80によるキャノピー上空のPAR測定値は、全球PARの値となります。緯度と時間帯がわかっているため、潜在放射量(地球大気圏外の水平面上の放射量)を計算することができます。これら2つの測定値の比は、Spittersらが行ったのと同様に、太陽ビーム中の全PARの割合に関係します。LP-80での手順は以下の通りです。
- プローブに到達する潜在的なPARの割合であるr を計算する。これは、PARの "太陽定数 "に天頂角のコサインを掛け、キャノピー上のPARの読みで割ったものである。PARの "太陽定数 "は2550 μmol/m2/sと仮定する。
- r の値が0.82以上の場合は晴天、0.2以下の場合は完全拡散天とする。
- r は、データから導かれる以下の経験的多項式で、ビーム率を計算するために使用される。
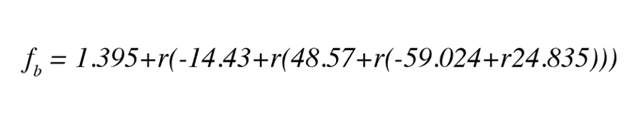
この計算を行うためのマクロは、以下の付録に記載されています。
LP-80理論で時間と労力を節約
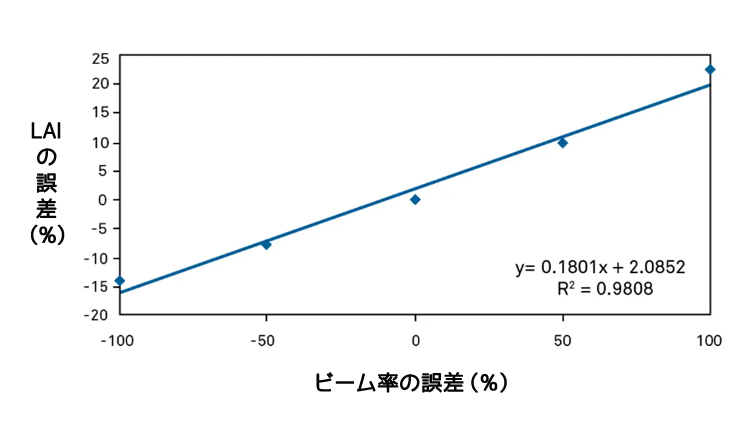
この方法は、ƒb を直接測定するよりも、よほど慎重に行えば精度は落ちるものの、キャノピー遮断やLAIを測定しようとすると、ƒb の直接測定を日常的に行うことは困難です。実際、LP-80で使用されている近似的な方法によってもたらされる誤差は、他の測定の誤差と比較して一般的に小さいものです。次のグラフは、すべてのLAI計算に一定のビーム率0.4を使用したと仮定し、ビーム分率の推定誤差の関数としてLAIの誤差を示したものです。
この誤差はLAIとは無関係です。計算は天頂角30度の場合です。天頂角が大きいと誤差は小さくなります。このグラフから、LAIの誤差は常に±20%より小さいことがわかります。ビーム率が10%の誤差の場合、LAIの誤差は2%程度です。LP-80 のビーム率の計算方法は条件によって異なるので、どの程度の誤差があるかは分かりませんが、10-20% 程度の誤差があると思われます。したがって、これがLAI計算にもたらす誤差は2~4%の範囲であり、LAIの測定における空間的変動による不確かさよりもかなり小さいです。
参考文献
Spitters, C. J. T., H. A. J. M. Toussaint, and J. Goudriaan. “Separating the diffuse and direct component of global radiation and its implications for modeling canopy photosynthesis part I. components of incoming radiation.” Agricultural and Forest Meteorology 38, no. 1-3 (1986): 217-229. Article link.
ビーム率を計算するための Visual BASIC マクロ
- Function BeamFraction(Zenith As Single, PAR As Single) As Single
- Const pi = 3.14159
- Dim r As Single, b As Single
- Zenith = Zenith * pi / 180
- If Zenith > 1.5 Then
- b = 0# 'nighttime
- Else
- r = PAR / (2550# * Cos(Zenith)) '600 w/m2 * 4.25 umol/w/m2 (.235 MJ/mol)(600 is potential PAR)
- If r > 0.82 Then r = 0.82
- If r < 0.2 Then r = 0.2
- b = 48.57 + r * (-59.024 + r * 24.835)
- b = 1.395 + r * (-14.43 + r * b)
- End If
- BeamFraction = b
- End Function


